INEQUALITIES 3

Adding or Subtracting a Value

We can often solve inequalities by adding (or subtracting) a number from both sides (just as in Introduction to Algebra), like this:

Example 1 :

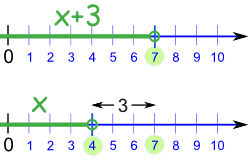
Solve: x + 3 < 7

If we subtract 3 from both sides, we get:

x + 3 - 3 < 7 - 3    

x < 4

And that is our solution: x < 4
In other words, x can be any value less than 4.

What did we do?

 And that works well for adding and subtracting, because if we add (or subtract) the same amount from both sides, it does not affect the inequality.

Example 2: 

Alex has more coins than Billy. If both Alex and Billy get three more coins each, Alex will still have more coins than Billy.

What If I Solve It, But "x" Is On The Right?

No matter, just swap sides, but reverse the sign so it still "points at" the correct value!

Example 3: 

12 < x + 5
If we subtract 5 from both sides, we get:

12 - 5 < x + 5 - 5    

7 < x

That is a solution!
But it is normal to put "x" on the left hand side ...

... so let us flip sides (and the inequality sign!):

x > 7

Do you see how the inequality sign still "points at" the smaller value (7) ?
And that is our solution: x > 7

 Note: "x" can be on the right, but people usually like to see it on the left hand side.

Exercise :

Solve x + 5 < 12